Multiplication, Mice, and Math practices

I can hardly believe October is here!  With cooler weather comes one of the concepts that students are most excited to learn about in 3rd grade...multiplication!  I've written before about how important the idea of multiplication is in 3rd grade, and how the progression of concepts eventually leads to the concept of the Distributive Property, but did you know that multiplicative concepts encompass an entire critical area in 3rd grade Common Core?!?!  Let's just think about that for a second and 'word-nerd' it-- According to dictionary.com:

critical-adj 

1.	containing or making severe or negative judgments
2.	containing careful or analytical evaluations: a critical dissertation
3.	of or involving a critic or criticism
4.	of or forming a crisis; crucial; decisive: a critical operation
5.	urgently needed: critical medical supplies
6.	informal  so seriously injured or ill as to be in danger of dying
7.	physics  of, denoting, or concerned with a state in which the properties of a system undergo an abrupt change: a critical temperature
8.	go critical  (of a nuclear power station or reactor) to reach a state in which a nuclear-fission chain reaction becomes self-sustaining

Basically, with the help of multiplication, our 3rd graders will reach a state of nuclear-fission!!  But in all seriousness, I think the fifth definition sums it up best, multiplicative concepts in 3rd grade are "urgently needed" so that our students have a foundation so strong enough to support and deepen their understanding of later concepts and grades.

So, obviously, multiplication is important, but how do we, as teachers, build that strong foundation?  For us, we start by thinking about the math ideas necessary to truly understand the concept of multiplication.  Together with my amazing third grade team, we mapped out what we believe to be a logical progression of ideas that would support the bigger idea of multiplication in 3rd grade.  Here is what we came up with: repeated addition, skip counting, equal groups, arrays, area models (area as additive, then multiplicative), and eventually, the concrete proof of the Distributive Property.  In reality, these ideas will be the primary focus of our math instruction, and will take us until about mid-November until we move on to other (related) concepts.

We are currently in our third week of building multiplicative concepts in 3rd grade, and I can definitely say that my students are using a very wide variety of strategies to solve our multiplication math tasks.  Today, we completed a "Mouse Problem" in which students were asked to select a number of mice to "buy" from the pet store.  Each year, their mouse population increases in size (2nd year, population doubles, 3rd year it triples, and so on), and students were asked to figure out how many mice they would have by the 5th year.


Skip Counting in parts

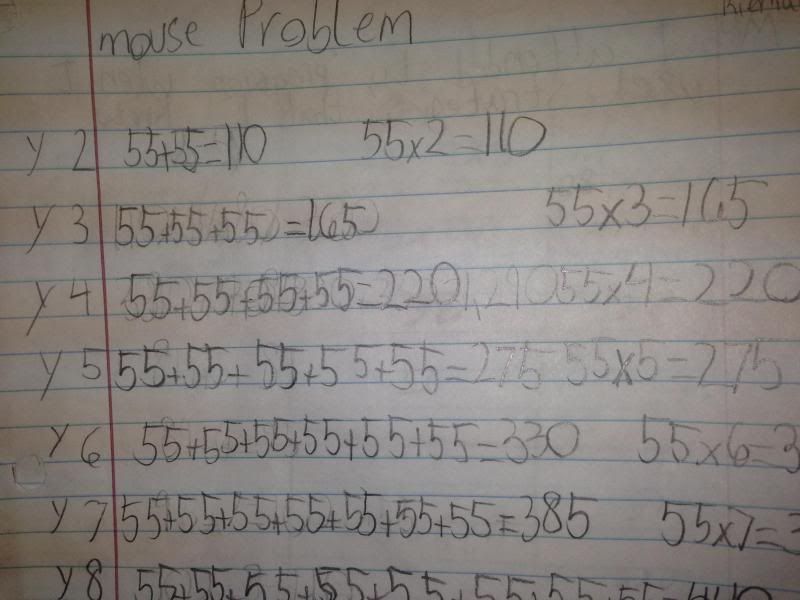Multiplication with repeated addition

And some of our progress with Math Practice Standards...



This last pic is my fav because it is SO 3rd grade.  This student had a very interesting patterning strategy to find their products, and was extremely ambitious in the original number of mice they started with (501), but check out the "math" vocabulary!  I LOVE "sixdupal" and the others that follow it, and I can definitely appreciate an attempt at attending to precision in our mathematics vocabulary.

Now that October is here, what are you working on in your classroom?

The Distributive Property

A few years ago, I never would have imagined spending months and months developing and building upon multiplication concepts, but that is exactly what I feel like we have done this year.  We've moved through multiplication as equal groups, repeated addition, arrays, skip-counting, area models, and partial products, and we aren't done yet.  It's been a big investment, but I don't regret a single minute of it, because I am seeing major growth in my students. 

The Common Core says that third graders are expected to be able to "apply properties of operations to multiply and divide", which includes the Distributive Property (3.OA.B.5).  The idea of the distributive property is HUGE in developing a deep conceptual understanding of multiplication for kids, but if you are anything like me, you didn't "learn" the Distributive Property until middle school (FOIL, anyone?).  What might this look like in 3rd grade?!  So the following is my experience introducing distributive property to 8 and 9 year old kiddos.  

We developed a context for this idea through area problems, which seemed like a natural starting point.  I created rectangular "brownie pans" with tape on each of my tables with various dimensions.  One of the important pieces in getting students to think about and eventually use the Distributive Property is creating a need to break apart your factors, so I intentionally made the dimensions of the "brownie pans" large enough to do just that.  I posed the following problem, and let them get to work:  

"Your busy teacher was asked to bake brownies bites for an upcoming bake sale.  Because she is so busy, she only has time to bake one batch of brownies.  She needs your help in deciding which cookie sheet to use that will allow her to make the most brownie bites in a single batch.  Use everything you know about finding area to figure out how many 1-square inch brownie bites she can make if she uses the baking sheet outlined on your desk.  As we know, things don’t always turn out how we expect them to, so be ready for anything!  Attend to precision, and be prepared to share your findings with the class!"

Five of six groups began tiling their rectangle almost immediately, as tiling to find area is one method that students had been exposed to.  After spending five minutes furiously tiling their area, it quickly became apparent that counting their tiles, or even repeatedly adding their rows or columns, would not be an efficient way to find the total area.  Thankfully, they also had been exposed to an area model for multiplication, so multiplying it would be...if they only knew what to do with these big numbers.  The final group measured their dimensions with a yardstick, and were immediately stuck with two numbers too large to multiply using strategies they had previously learned.  This "stuckness" was exactly what I was hoping for, because it created a need to try something new.

As I made my way from group to group, I heard numerous, "I don't know how to skip count by 19's!!" and "We haven't learned how to multiply big numbers yet!".  But I also heard, "Ok, let's cut the pan in half, and you do that side, and we will figure out this side", and "Let's take out the 10 x10 piece, because that's 100 brownies, then we can solve what is left".  Problem solvers in action!  Not all groups were so logical in the ways in which they broke-apart their area, so I had to be mindful in questioning students to get them to think about meaningful ways to break-apart their dimensions (landmark numbers, tens, fives, etc.).  

Students used rulers to "cut" the brownies into chunks, post-it notes to keep track of the area of each part, and worked together to present their findings on their recording sheet.  All groups had a chance to share their work, and we discussed the ways in which they chose to break-apart their large area or dimensions into smaller pieces.  We also talked about how this idea of taking large factors and decomposing them into smaller parts, multiplying, then adding all the parts back together, can be used to multiply bigger numbers.  

We have since used the Distributive Property time and time again in many different instances, most recently in finding the area of a football field.  

     So there you have it, my experience introducing 3rd graders to the Distributive Property. The DP is a huge concept, and this lesson just scratched the surface.  I am very pleased with how my students responded to that scratch.

Happy Weekend!